안녕하세요

엠포스 데이터랩입니다.
해당 데이터 분석 방법론 카테고리에서 정말 오랜만에 인사드리네요.
방법론에서 좀 더 자주 찾아뵐 수 있도록 할께요!! 🙂

데이터를 분석해보는 데에 있어서 조금이나마 도움을 드리고자
이번에 소개드릴 분석 방법은 “시계열 클러스터링” 인데요.
시계열 클러스터링을 R로 구현하는 방법과 분석의 의미에 대해 알아보겠습니다.

시계열 클러스터링은 시간성을 가진 개체들의 데이터를 묶어주는 방법인데요.
이에 따라 개체별로 가지는 추이 혹은 트렌드를 살펴볼 수 있습니다.

예시를 들면, 수백개의 다양한 상품들에 대한 구매 데이터가 있다면.
요즘 자주 구매하는 상품들, 구매성이 떨어지는 상품의 추이를 각각 분류하여 확인이 가능합니다!

사실 클러스터링에 대해서는 정말 많이 들어보셨을 것 같은데요!

클러스터링(Clustering)이란 군집 분석이라고도 하며, 비지도 분류 학습으로
이는 데이터를 분류하는 데에 있어 가장 많이 쓰이는 부분입니다.

클러스터링을 주로 쓰는 목적에 대해서는 방대한 데이터를 가진 “개체”들을
특정한 “기준”을 통해서 각 데이터들을 “군집화” 시키는 방법으로
각각 군집을 가진 개체들의 특성과 분포 등을 살펴보는데에 주로 사용합니다.

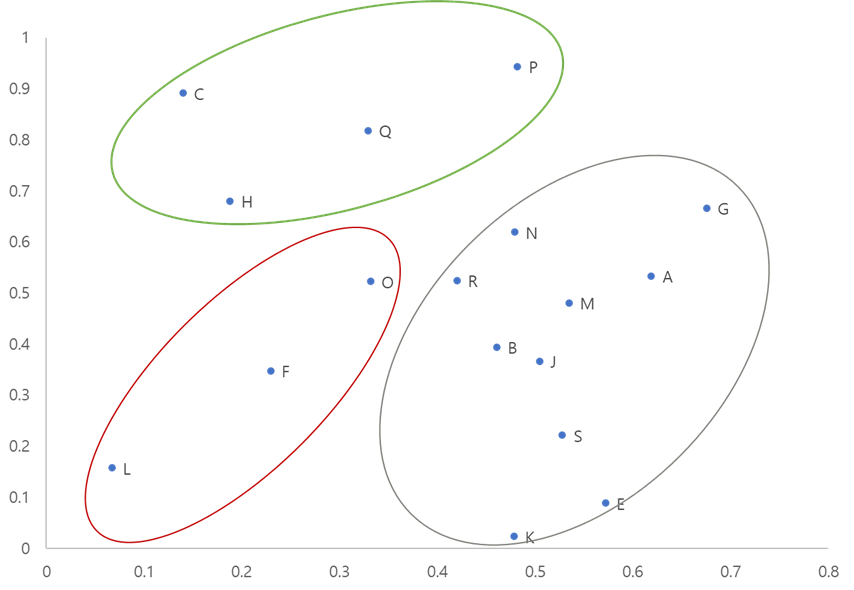
그림1의 경우 클러스터링을 접해보셨다면, 흔히 보는 예시로 생각되는데요.

그림 1과 같이 알파벳(A,B,C…)의 개체들이 특정 값에 분포해 있을 때,
이를 n개의 그룹으로 “묶어주는” 것이 클러스터링의 역할이라고 할 수 있는데요.

그렇게 해서 클러스터 내의 개체들은 서로 “비슷한” 속성을 가지고,
서로 다른 클러스터 간의 개체들은 서로 “다른” 속성으로
상대적으로 먼 거리를 두어 클러스터링 하는 것이 목표라고 할 수 있겠습니다!

방금까지 클러스터링의 내용을 간단히 말씀드렸다면,
그러면 시계열 클러스터링(이하 : tsclust)은 무엇인지 본격적으로 말씀을 드리고자 하는데요.

“시계열”을 가진  즉, 시간을 가진 데이터들에 대해서도 분류 “기준”을 통해
속성이 비슷한 동적인 개체들끼리 분류하여 군집화 하는 것이라고 말씀 드릴 수 있습니다.

그림1의 예시의 경우 개체들은 X 변수와 Y 변수로 이루어진 정적인(static) 데이터라고 한다면
시계열을 가진 데이터들은 X변수와 Y변수 뿐 아니라 시간에 따라 움직이는 동적인(Dynamic) 데이터로 말합니다.

그렇게 해서 tsclust는 dtw라는 거리측정을 통해,
“시계열에 따른 추이가 비슷한 개체들끼리 분류”  가 분석의 로직이라고 말씀드릴 수 있겠네요 ^^

tsclust의 간략한 구현으로 이해를 돕기 위해
네이버 쇼핑인사이트에서 화장품/미용 업종의 인기검색 상품 300위의 클릭지수 일간 데이터를 수집하고,
해당 키워드들의 일간 쇼핑 클릭량을 2018년 1월부터 2020년 12월까지 수집하여 시계열 클러스터링을 적용하겠습니다.

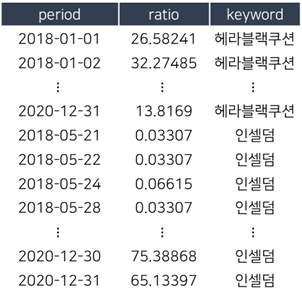
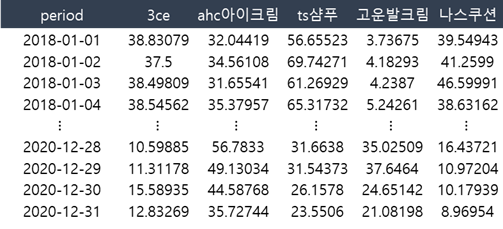
위 데이터를 통해서 tsclust의 예시를 보여드릴텐데요.
해당 데이터를 불러온 뒤, 그림3과 같은 데이터의 구조 변경이 필요합니다.

tst<-read_excel(“Beauty_ShoppingClick.xlsx”,
sheet = 1,
col_names = T,
col_types = “guess”,
na = “-”
)

이 후 reshape2 패키지를 이용하여 데이터의 구조 변경
df_dcast_tst <- dcast(tst, period~keyword, value.var = “ratio”, sum,fill=0)

그 다음으로 period의 시간 데이터를 분리하고 데이터를 tsclust 구조에 맞춰주시면 됩니다.

각 상품 키워드의 데이터들을 정규화 작업을 진행해주는데요.

normalized = function(x){
m = mean(x)
s = sd(x)
n = (x-m)/s
return(n)
}

normalized_search = lapply(data_list,function(x) normalized(x))

그 다음 정규화 작업이 끝났다면 이 데이터를 dtwclust()의 tsclust()에 집어넣어주세요!

시계열 클러스터링을 구현하기 위해, 최적의 클러스터 갯수를 찾아보려고 하는데요.
2개에서 10개까지 dtw_basic 측정 방법으로 갯수를 찾아보겠습니다.

pc.dtw <- tsclust(normalized_search,
type=”partitional”,
centroid = “pam”,
k = 2L:10L,
distance = “dtw_basic”,
seed=1234,
trace=T,
args = tsclust_args(dist = list(window.size = 60L))

)

해당 클러스터 학습이 완료되면,
평가 지표를 이용해 몇개의 클러스터 분류가 “적합”한지 7개의 지표를 통해 확인합니다.

eval_clust<-sapply(pc.dtw, cvi) # 지표 값 데이터 저장

# 클러스터 최적화 갯수의 지표 값 그래프
plot(eval_clust[1,],type=”l”, main=”sil index”, xlab=”The number of clusters”, ylab=”극댓값 부분을 찾아주세요“)

plot(eval_clust[4,],type=”l”, main=”DB index”, xlab=”The number of clusters”, ylab=”극솟값 부분을 찾아주세요“)

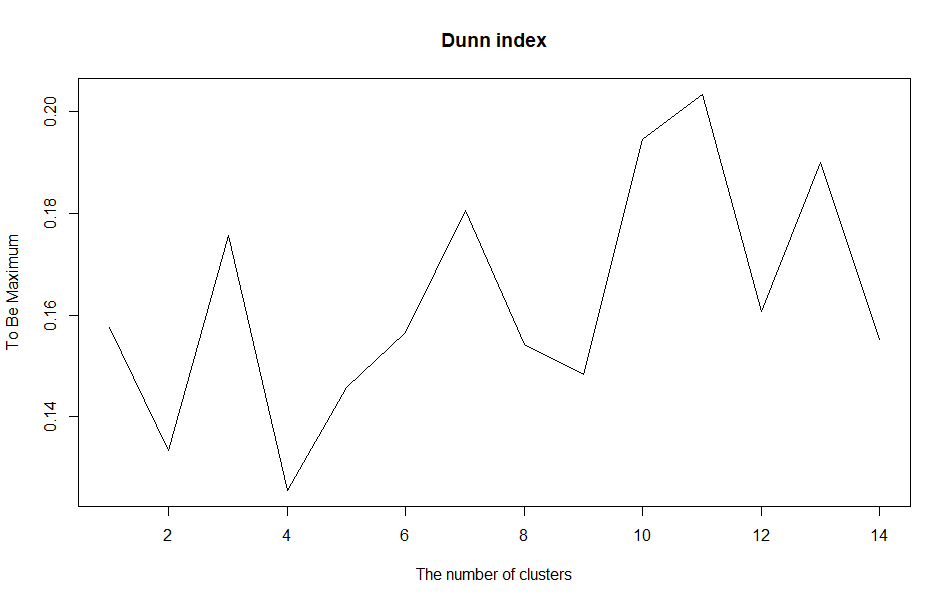
예시로 Dunn Inxdex의 경우 최댓값으로 지향하며,
클러스터 갯수(k)는 극댓값을 가진 구간은 k= 3, 7, 11 등으로 볼 수 있습니다.

각 그래프별 최댓값 지향(극댓값)과 최솟값 지향(극솟값)으로 지표를 살펴보신다음 최적의 클러스터 갯수를 선정하시면 됩니다.

이 외에도 지표 방법인 main = [“SF index”, “CH index”, “DB index”, “MDB index”, “COP index”] 등

클러스터링 갯수의 최적화를 위해, 총 7가지의 지표를 사용할 수 있습니다.
7가지 지표를 모두 쓰실 필요는 없으시되 최댓값과 최솟값을 지향하는 지표로
쓰시면 됩니다.

dtw_cluster = tsclust(normalized_search, type=”partitional”,k=???,
distance=”dtw_basic”,centroid = “pam”,seed=1234,trace=T,
args = tsclust_args(dist = list(window.size = 60)))

위와 같은 클러스터 학습을 시켜주면 아래와 같이 그래프로 나타낼 때,
시계열에 따른 개체들이 클러스터로 묶은 데이터를 보여줍니다.

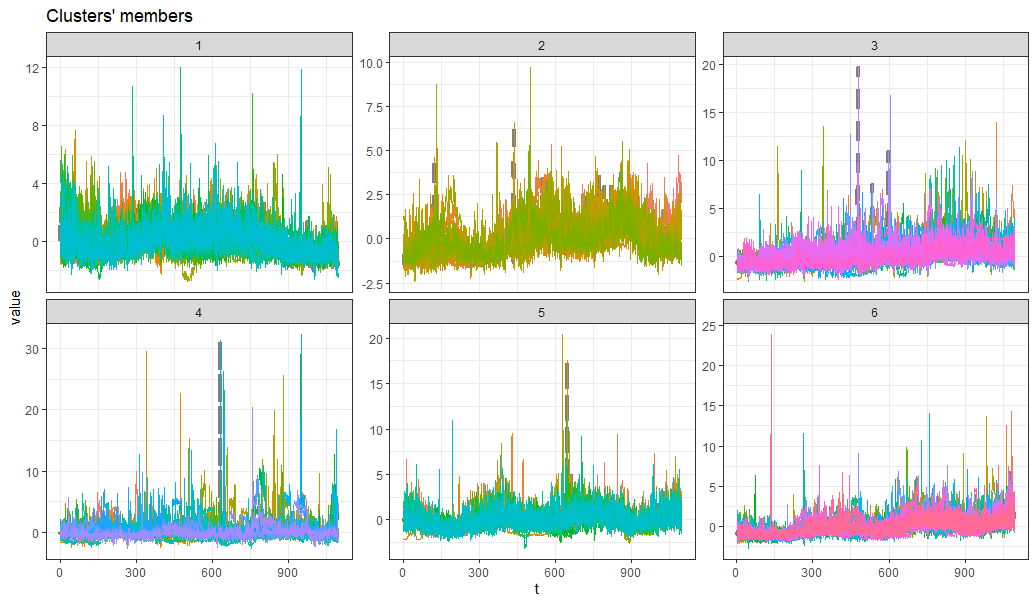
1번 클러스터의 경우 쇼핑 클릭추이가 하락하는 개체들이 보이며,
2번, 6번의 경우 꾸준히 상승하고 있는 클릭 추이를 보이네요.

해당 윗그림에서는 몇몇 클릭 지수가 매우 높은 값으로 크게 튄 개체들이 있는데,
이들에 대해서는 개별로 값을 확인할 필요가 있는 것 같습니다.

1번 클러스터의 경우 지속적인 하락이 보이는 개체들로 이루어진 것 같은데,
1번 클러스터의 centroid를 살펴보겠습니다.

#클러스터 centroids data 확인
dtw_cluster@centroids

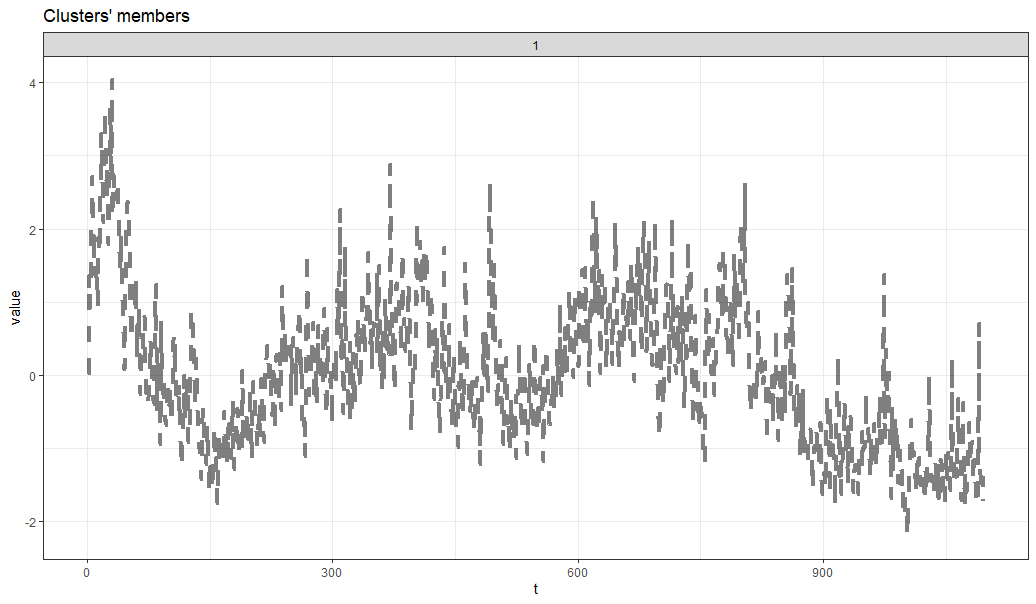
그림6의 경우 1번 클러스터 Centroid의 시계열 데이터입니다.
맵릭스틱이라는 상품 키워드가 지속적으로 하락 추세를 보이며
특히 2020년 들어서는 하락폭이 좀 더 크게 나타나는 등으로 살펴볼 수 있습니다.

위처럼 시계열 클러스터링의 구현 자체는 R프로그래밍의 패키지(dtwclust)를
이용한 tsclust() 함수로 금방 도출이 됩니다.

해당 과정에 추가적으로 지표값 최적화와 데이터 대치값 변환, 파라미터 선정
결과값 저장과 클러스터 내부의 개체 확인 등등을 선택적으로 작업해주시며,
(이 부분이 가장 오래 걸리는 일이기도 하죠^^;;;;)
이 후 프로젝트의 목적에 맞게 추가적인 심층적인 분석 방법을 설계 하시면 됩니다.

시계열 클러스터링에 적합한 데이터의 특성
기본적으로 당연히 동적인 데이터의 특성을 가지고 있어야 하며,

시간에 민감한 데이터를 가진 데이터들이라면 더욱 알고리즘의 결과는 더욱 유의미해집니다.

예를 들면, 여름이나 겨울에 특이한 패턴이 형성되는 시즌성을 가진 데이터처럼
“트렌드”를 크게 타는 데이터라면 그 패턴들을 개체별로 묶어 볼 수 있습니다.

추가적으로 최소한으로 필요한 개념인
Centroids와 DTW에 대한 개념을 끝으로 내용을 마무리하겠습니다.

Centroids란?

Centroids는 각 클러스터의 중심점이라고 말씀드릴 수 있습니다.
위 예시 처럼 k=6으로 6개의 클러스터로 분류하고자 할 때
6개 각각의 거리 측정 기준값이 있어야하는데요. 이게 Centroids입니다!
(6개 클러스터라면 6개의 Centroids가 필요하겠죠? )

dtwclust 패키지와 tsclust()에 내장된 함수의 Centroids 선정 방법은
“임의 선정”입니다. (샘플링을 통해 더 나은 Centroids를 선정합니다.)
임의 선정 후 각 센트로이드의 거리 측정이 “가까운” 개체들을 찾아 묶어줍니다.

위 그림에서 보여드린 1번 클러스터의 경우

“맥 립스틱”의 시계열 데이터를 기준으로 다른 키워드의 시계열 데이터와
유사한 개체 들을 1번 클러스터로 묶어주는 역할 입니다.

시계열 클러스터의 Centroids가 의미하는 바는 “각 클러스터의 대표 분포 개체”이고
해당 분포와 “비슷한 분포”를 가진 개체끼리 분류 한다고 볼 수 있습니다.

DTW(Dynamic Time Warping)이란?

위 설명에서 “비슷한 분포”라고 말씀을 드렸는데요

기본적으로 클러스터링에 적용되는 거리 측정 방법은
보통 유클리디안 거리를 통해서 개체들의 거리를 측정하곤 합니다.
하지만 시계열 클러스터링의 경우는 DTW 방법을 적용할 수 있습니다.
(distance = “dtw_basic” )

DTW는 동적 시간 왜곡으로 말하며 주로 시간을 가진 개체의 데이터 추이가
어떤 개체의 흐름과 비슷한 패턴을 가지는지 비교하는데요.
주로 주파수의 측정. 음성 인식 비교 서비스와 같은 곳에 자주 쓰인다고 합니다.

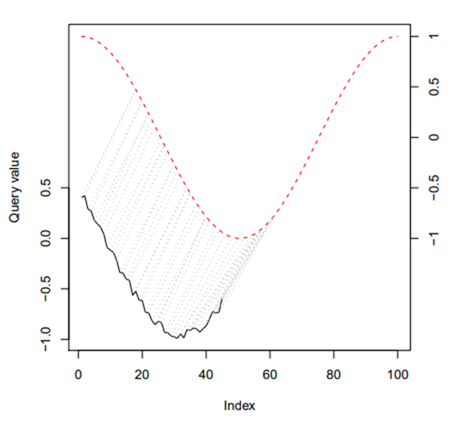
위 그림에서 설명을 드리자면 위 빨간색 점선 그래프와
아래 검정 그래프의 경우 index 값은 서로 다른데요.
하지만, DTW를 통해서 index 값이 다르더라도
“추이와 변화하는 지점이 일치하다면 서로 비슷하다”라는 것이
DTW 사용의 주목적이라고 말씀드릴 수 있습니다.

해당 tsclust의 파라미터별 자세한 내용은
https://www.jstatsoft.org/ 에서 제공한 tsclust 라이브러리의 공식 문서와
DTW에 대한 보다 상세한 내용이 담긴 문서가 있는데요.

아래 문서를 참고하시면
알고리즘의 이해와 구현에 대해 더욱 도움 되실 것 같습니다.